Barangkali Teorema Phytagoras sudah tidak asing lagi bagi kita, bahkan mungkin sudah sering menerapkannya dalam kehidupan sehari-hari. Diantara sekian banyak teorema-teorema yang ada dalam matematika, teorema ini merupakan salah satu teorema yang cukup terkenal.
Namun jika ada diantara kita yang belum tahu atau lupa teorema tersebut, dapat melihat kembali teorema tersebut. Adapun teorema tersebut sebagai berikut:
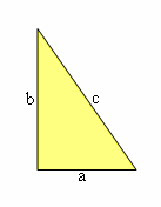
Perhatikan segitiga siku-siku dibawah ini :
c2 = a2 + b2
dari persamaan tersebut juga dapat dihasilkan persamaan
a2 = c2 – b2
atau
b2 = c2 – a2
Kenapa bisa ditarik persamaan seperti itu? Apa benar seperti itu?
Seandainya pertanyaan-pertanyaan tersebut muncul, barangkali jawabannya adalah pembuktian dari Teorema tersebut. Jika Teorema tersebut tidak terbukti, atau ada satu kasus yang membuat kontradiksi maka Teorema tersebut akan gugur/ tidak berlaku lagi.
Nah, bagaimana dengan Teorema Phytagoras? Ada beberapa cara membuktikan Teorema tersebut. Salah satunya adalah dengan cara berikut ini.
Perhatikan Gambar dibawah ini.
Pada gambar diatas, terdapat 4 segitiga siku-siku yang sebangun dan sama besar, persegi dengan panjang sisi c dan persegi dengan panjang sisi a + b. Luas Segitiga siku-siku tersebut masing-masing adalah
, luas persegi yang didalam (warna pink) adalah c2 dan luas persegi yang besar (yang terluar) adalah (a + b)2 = a2 + 2ab + b2.
Dari gambar bidang tersebut, dapat kita peroleh persamaan yaitu :
Luas persegi yang terluar = luas persegi yang didalam + 4 luas segitiga siku-siku.
a2 + 2ab + b2 = c2 + 2 ab
a2 + 2ab + b2 – 2ab = c2
a2 + b2 = c2
Pembuktian selesai. Dengan demikian, terbukti c2 = a2 + b2
Tidak ada komentar:
Posting Komentar